OpenCV笔记

一. 图像预处理

 

1. 图像显示与存储

1.1 颜色空间

 

• 颜色空间（RGB）

1. 加法混色
2. 三通道：RGB
3. 一个像素的颜色值：（b,g,r）
4. 取值范围：[0,255] or [0.0,1.0]

• 颜色空间（CMY(K)）

1. 减法混色，用于印刷

2. 四通道

   • Cyan通道
   • Magenta通道
   • Yellow通道
   • black通道（key通道）

3. 一个像素的颜色值：（c,m,y,k）

4. 取值范围：[0,255] or [0.0,1.0]

 

• 颜色空间（HSV）

1. 人类视觉概念，画家配色

2. 三要素

   • H/Hue：色调，颜色种类
   • S/Saturation：饱和度，颜色的纯度
   • V/Value：明度，颜色明亮度

3. 一个像素的颜色值：（h,s,v）

4. 取值范围：[0,255] or [0.0,1.0]

 

• 颜色空间（CIE-XYZ）

1. 国际照明协会1931年提出

2. 基于人类颜色视觉的直接测定

3. 其他颜色空间基础

4. 人类视觉系统-视锥细胞

   • 短波（S，420-440nm）
   • 中波（M，530-540nm）
   • 长波（L，560-580nm）

5. 三色刺激值通道

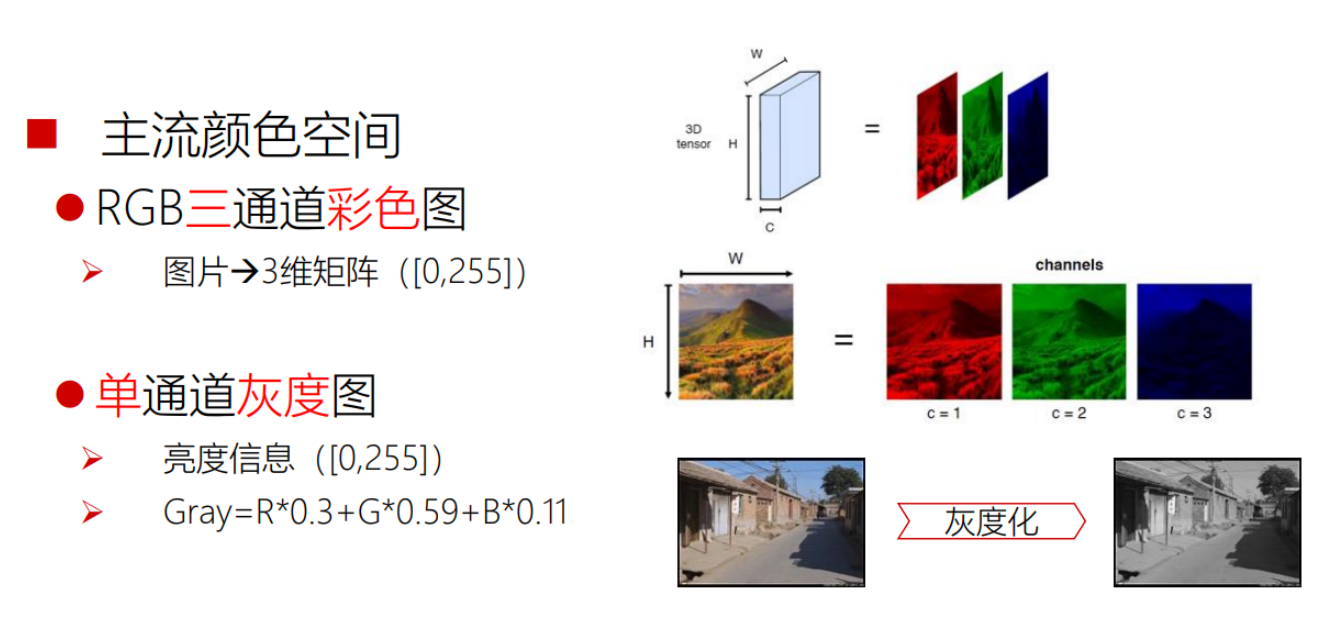
（三通道彩色图片到单通道灰度图是单向变换）

1.2 图片存储原理

1. 常见的存储的格式有：bmp, jpg, png, tiff, gif, pcx, tga, exif, fpx, svg, psd, cdr, pcd, dxf, ufo, eps, ai, raw, WMF, webp等
2. BMP：采用位映射存储格式，不采用其他任何压缩，所占用的空间很大。
3. JPG：最常见的有损压缩格式，能够将图像压缩到很小的空间，压缩比 可达10:1到40:1之间。
4. GIF：基于LZW算法的连续色调的无损压缩格式，其压缩率一般在50% 左右。
5. PNG：是比较新的图像文件格式，能够提供长度比GIF小30%的无损压 缩图像文件。

 

 

2. CLAHE 对比度受限的直方图自动均衡

2.1 图像处理方法分属

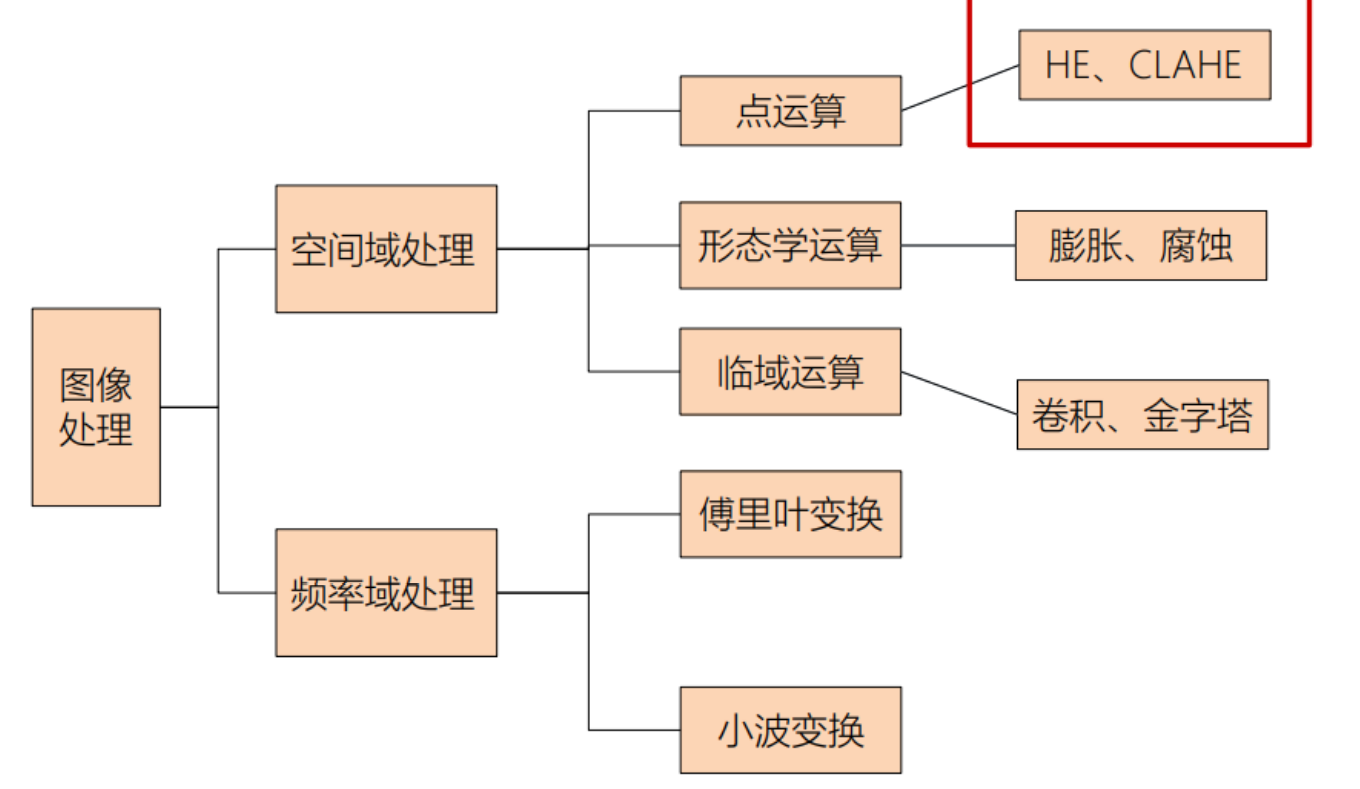
2.2 直方图均衡

2.2.1 定义

直方图均衡(Histogram Equalization)是(图像处理)领域中利用直方图对对比度进行调整的方法.

顾名思义, 直方图均衡是将直方图的分布(概率密度)调整为均匀分布。

2.2.2 为什么要做直方图均衡

根据信息论，信息的熵越大，包含的信息也就越多，熵的计算公式如下：

只有当$p(x_i)$ 为均匀分布时，熵的值最大，对应到图像上，当直方图均匀分布时，图像对比度最大。如下图所示：

蓝色为原始图像直方图，绿色为均衡后直方图，对应的处理后图像为：

可以直观地看出，直方图均衡处理后，图像变得更加清晰了。

直方图均衡化通常用来增加许多图像的局部对比度，尤其是当图像的有用数据的对比度相当接近的时候。直方图均衡化以后，亮度可以更好地在直方图上分布。这样就可以用于增强局部的对比度而不影响整体的对比度，直方图均衡化通过有效的扩展常用的亮度来实现这种功能。

直方图均衡化在实质上是对图像进行非线性拉伸。重新分配各个灰度单位中的像素点数量，使一定灰度范围像素点数量的值大致相等。

2.2.3 特征提取方法 - 直方图

• 对图片数据/特征分布的一种统计

  • 灰度，颜色
  • 梯度/边缘，形状，纹理
  • 局部特征点，视觉词汇

• 区间（bin）

  • 具有一定的统计或物理意义
  • 一种数据或特征的代表
  • 需要预定义或基于数据进行学习
  • 数值是一种统计量：概率，频数，特定积累

• 对数据空间(bin)进行量化

2.2.4 如何做直方图均衡

通常做直方图均值有以下几个步骤

1. 统计图像的直方图，归一化到[0.1]

2. 计算映射函数

式中，$H,W$分别为图像的高和宽，$n_k$表示灰度值为$r_k$的像素个数，$s_k$为变换后的灰度值，$T(r_k)$为映射函数，计算过程使用了累计直方图

3. 利用得到的映射函数，对图像进行处理
4. 对于RGB图像，可以转到HSV空间，对V通道进行均衡后，转回RGB空间，如下图所示结果：

2.2.5 为什么可以这样处理

设原始直方图分布为：$p_r(r_k)$

均衡化后的直方图分布为：$p_s(s_k)=\frac{1}{L-1}$

映射函数为：$s_k=T(r_k)$

这里映射函数必须为单调递增函数，满足：$\int_{0}^{s_k}p_s(s)ds=\int_{0}^{r_k}p_r(r)dr$

就是说对应区域间内像素点的总数总是一样的，如下图红色区域所示：

 

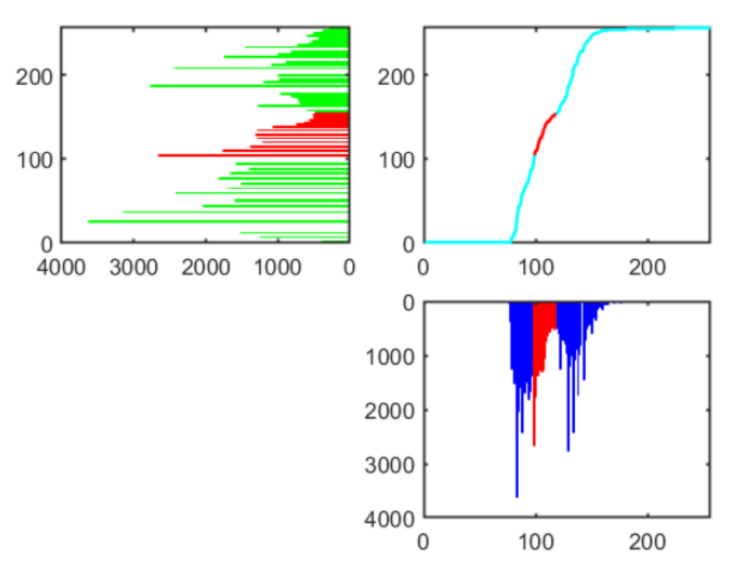
我们将$p_s(s_k)=\frac{1}{L-1}$代入$\int_{0}^{s_k}p_s(s)ds=\int_{0}^{r_k}p_r(r)dr$，则有：

与之所对应的离散形式的公式为$s_k=T(r_k)=(L-1)\sum_{j=0}^{k}p_r(r_j)$

 

2.2.6 存在的问题

1. 如果映射函数为$s_k=(L-1)\int_{0}^{r_k}P_r(r)dr$，这个是连续形式，在这个情况下映射是可逆的，但是变成离散形式后映射就不可逆了。
2. 映射变换会丢失信息，对出现比例很少的灰度进行合并，会丢失部分的细节。
3. 对于占比例较多的灰度，则会将其拉伸，而导致其占据了更多的灰度，压缩了其他的灰度。

 

2.2.7 改进

直方图均衡过度地强调了灰度个数的重要性，对数量多的灰度过度地进行了增强，而图像中，比例不多的灰度往往更重要，因此改进的方向就是对数量较多的灰度进行减少影响。可以如何改进呢？

我们可以对直方图进行截断，超出部分直接去除，从而减少灰度过多的带来的影响。那在此基础上，我们还可以将超出的部分均匀地加到直方图的每个bin上，拿着就是CLAHE了。

2.3 AHE

直方图均衡的经典算法对整幅图像的像素使用相同的变换，如果图像中包括明显亮的或是暗的区域，则经典算法作用有限。

自适应直方图均衡（AHE）算法通过对局部区域进行直方图均衡来解决上述问题。步骤如下：

• 移动模板在原始图片上按特定步长滑动；
• 每次移动后，模板区域内做直方图均衡，映射后的结果赋值给模板区域内所有的点；
• 每个点会有多次赋值，最终的取值为这些赋值的均值。

2.4 CLAHE

AHE会过度放大图像中相对均匀区域的噪音，可采用限制对比度自适应直方图均衡即CLAHE，与普通的自适应直方图均衡相比，CLAHE的不同地方在于直方图修剪的过程，用修剪后的直方图均衡图像时，图像的对比度会更自然。

2.4.1 CLAHE的原理

• 小黑点的灰度直接由映射函数计算得到；
• 粉色区域内点的灰度由映射函数计算而得；
• 绿色区域内点的灰度由相邻两块灰度映射值线性插值而得；
• 其他区域所有点的灰度由相邻4块的灰度映射值双线性插值而得。

2.4.2 CLAHE算法步骤

1. 图像分块，以块为单位；
2. 先计算直方图，然后修剪直方图，最后均衡；
3. 遍历操作各个图像块，进行块间的双线性插值；
4. 与原图做图层滤色混合操作。（可有可无）

2.5 线性插值

2.5.1 线性插值的定义

数学上定义：线性插值是指插值函数为一次多项式的插值方式，其在插值节点上的插值误差为0；在图片上，我们利用线性插值的算法，可以减少图片的锯齿，模糊。

2.5.2 单线性插值

单线性插值是在一个方向上进行线性插值，比如X方向；下面将根据维基百科说明如何进行线性插值：

假设我们已知坐标$(x_0,y_0)$与$(x_1,y_1)$，要得到$[x_0,x_1]$区间内某一位置$x$在直线上的值。根据图中所示，我们得到：

由于$x$值已知，所以可以从公式得到$y$的值：

已知$y$求$x$的过程与以上过程相同，只是$x$与$y$要进行交换。

2.5.3 双线性插值

双线性插值是有两个变量的插值函数的单线性插值扩展，核心思想是在两个方向上分别进行一次线性插值。

3. 膨胀腐蚀与开闭运算

3.1 图像处理分属

3.2 形态学运算

结构元素：设有两幅图像A、S。若A是被处理的对象，而S是用来处理A的，则称S为结构元素，通常是比较小的图像，S必须具有原点。

腐蚀：就是让原本位于图像原点的结构元素S在整个$Z^2$平面上进行移动，当S的原点平移至某一点时（假定这个点为z），S可以完全包含在A中，则所有这样的点z构成的集合，即为S对A的腐蚀图像。

膨胀：让原本位于图像原点的结构元素S在$Z^2$上移动，当自身原点平移至z点，S和A有交集，也就是说至少有一个元素是重叠的，这样的z点构成的集合也就是S对A的膨胀图像。

• 膨胀是对原图的目标部分进行膨胀，类似于领域扩张。
• 腐蚀是对原图的目标部分腐蚀，类似于领域被蚕食。

开运算：先腐蚀再膨胀。

闭运算：先膨胀再腐蚀。

通常，当有噪声的图像用阈值二值化后，所得到的边界是很不平滑的，物体区域具有一些错判的孔洞，背景区域散步着一些小的噪声物体，连续的开和闭运算可以显著的改善这种情况。

开运算使图像的轮廓变得光滑，断开狭窄的连接，消除毛刺和孤立点。闭运算同样使得轮廓变得光滑，它通常能够弥合狭窄的间断，填充小的孔洞。

注意：所有的形态学运算都是针对图像中的前景物体进行的。大多数软件将物体用黑色表示（灰度值为0），背景用白色表示（灰度值为255），如C++就遵循此规定。但是Matlab在二值图像形态学处理中，默认白色为前景，而黑色为背景。

3.3 代码实现

在这里我们使用如下图例进行演示：

 

import cv2
import numpy as np
import matplotlib.pyplot as plt

img = cv2.imread('test.png')
def cv_show(img):
    plt.imshow(cv2.cvtColor(img,cv2.COLOR_BGR2RGB))
    plt.show()

#腐蚀操作
kernel = np.ones((3,3),np.uint8)
test_erosion = cv2.erode(img,kernel,iterations = 1)
'''
cv2.erode(src,kernel,iterations)
src:输入图片
kernel:方框大小
iterations:迭代次数
'''
cv_show(test_erosion)

输出结果为：

#膨胀操作
kernel = np.ones((3,3),np.uint8)
test_dilate = cv2.dilate(img,kernel,iterations = 1)
'''
cv2.dilate(src,kernel,iterations)
src:输入图片
kernel:方框大小
iterations:迭代次数
'''
cv_show(test_dilate)

输出结果为：

#开运算：先腐蚀，再膨胀
kernel = np.ones((5,5),np.uint8)
opening = cv2.morphologyEx(img,cv2.MORPH_OPEN,kernel)
'''
cv2.morphologhEx(src,op,kernel)
src:输入图片
op: cv2.MORPH_OPEN:开运算
    cv2.MORPH_CLOSE:闭运算
    cv2.MORPH_GRADIENT:形态学梯度
    cv2.MORPH_TOPHAT:顶帽，突出比原轮廓亮的部分
    cv2.MORPH_BLACKHAT:黑帽，突出比原轮廓暗的地方
kernel:方框大小，核大小，滤波器
'''
cv_show(opening)

输出结果：

#闭运算：先膨胀，再腐蚀
kernel = np.ones((5,5),np.uint8)
closing = cv2.morphologyEx(img,cv2.MORPH_CLOSE,kernel)
cv_show(closing)

输出结果：

接下来我们使用如下图例来演示形态学的梯度运算。

#梯度= 膨胀-腐蚀
pie = cv2.imread('test2.png')
kernel = np.ones((7,7),np.uint8)
dilate = cv2.dilate(pie,kernel,iterations=5)
erosion = cv2.erode(pie,kernel,iterations=5)
res = np.hstack((dilate,erosion))
cv_show(res)

我们先对比一下膨胀与腐蚀的结果：

gradient = cv2.morphologyEx(pie,cv2.MORPH_GRADIENT,kernel)
cv_show(gradient)

输出结果为：

 

4. 滤波与边缘填充

4.1 图像处理方法分属

4.2 空间域处理及其变换

4.2.1 滤波与卷积的定义

滤波/卷积：在每个图片位置(x,y)上进行基于邻域的函数计算

图像处理中滤波和卷积是常用到的操作。两者在原理上相似，但是在实现的细节上存在一些区别。

4.2.2 滤波与卷积的区别

1. 滤波

简单来说，滤波操作就是图像对应像素与掩膜（mask）的乘积之和。如有一张图片和一个掩膜如下所示：

那么像素$(i,j)$的滤波后结果可以根据以下公式计算：

其中$G(i,j)$是图片中$(i,j)$位置像素经过滤波后的像素值。当掩膜中心$m5$位置移动到图像$(i,j)$像素位置时，图像$(i,j)$位置像素成为锚点。

滤波的步骤：

1. 对原始图像的边缘进行某种方式的填充（一般为0填充）
2. 将掩膜划过整幅图像，计算图像中每个像素点的滤波结果

按照这个步骤，假设我们有一个二维矩阵I，掩膜M，则滤波的结果如下：

2. 卷积

卷积的原理与滤波类似。但是有一些细小的区别。

卷积操作也是卷积核与图像对应位置的乘积和。但是卷积操作在做乘积之前需要先将卷积核翻转180°，之后再做乘积。

在此可以看出如果卷积核不是中心对称的，那么卷积和滤波操作将会得到完全不一样的结果，另外卷积操作会改变图像大小（损失图像边缘），所以为了保证卷积后图像大小与原图一致，常用的做法是在卷积操作之前对图像进行边缘填充。

 

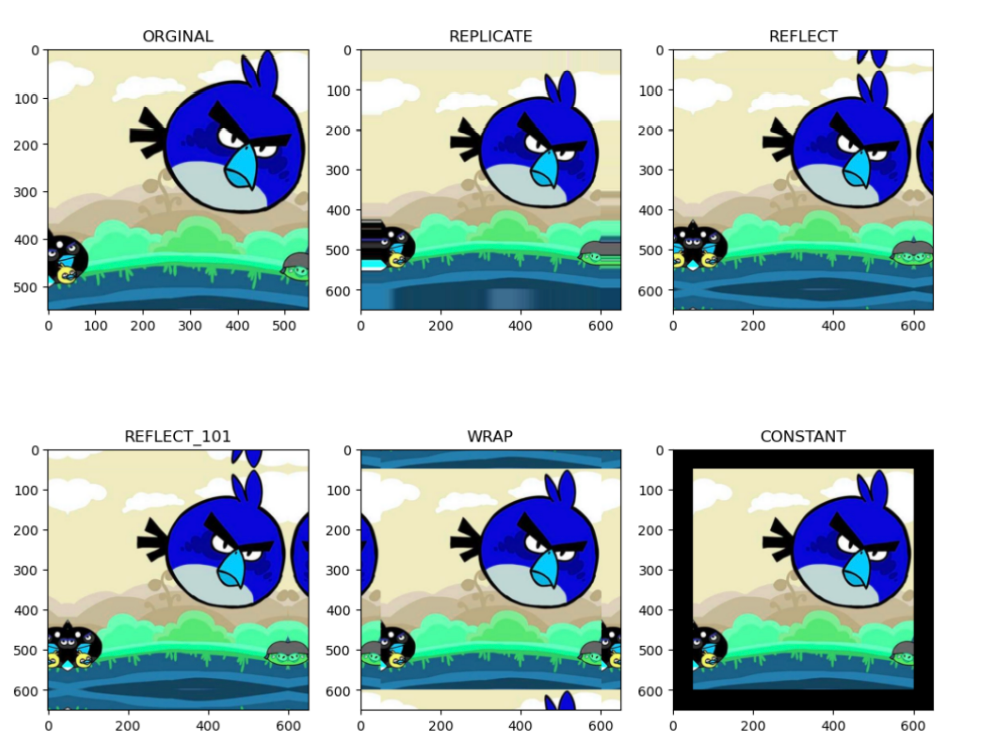
4.3 边缘填充策略

1. 补零（zero-padding）：在图像外面填充数层0元素（根据需要来确定层数）
2. 边界复制（replication）：复制边界的元素来进行填充，如下图例：

3. 镜像（reflection）
4. 块复制（wraparound）

4.4 边缘填充策略的代码实现

我们使用如下图例来进行演示：

import cv2
import numpy as np
import matplotlib.pyplot as plt

#定义上下左右四个方向的填充大小
top_size,bottom_size,left_size,right_size = (50,50,50,50)
#边界复制策略
replicate =cv2.copyMakeBorder(img,top_size,bottom_size,left_size,right_size,
                               borderType=cv2.BORDER_REPLICATE)
#镜像：对图像中的像素在两边进行复制如：fedcba|abcdefgh|hgfedcb
reflect = cv2.copyMakeBorder(img,top_size,bottom_size,left_size,right_size,
                             cv2.BORDER_REFLECT)
#镜像：以最边缘像素为轴，如：gfedcb|abcdefgh|gfedcba
reflect101=cv2.copyMakeBorder(img,top_size,bottom_size,left_size,right_size,
                              cv2.BORDER_REFLECT_101)
#块复制，如：cdefgh|abcdefgh|abcdefg
wrap = cv2.copyMakeBorder(img,top_size,bottom_size,left_size,right_size,
                          cv2.BORDER_WRAP)
#常量法，常数值填充
constant=cv2.copyMakeBorder(img,top_size,bottom_size,left_size,right_size,
                            cv2.BORDER_CONSTANT,value=0)

plt.subplot(231),plt.imshow(img,'gray'),plt.title('ORGINAL')
plt.subplot(232),plt.imshow(replicate,'gray'),plt.title('REPLICATE')
plt.subplot(233),plt.imshow(reflect,'gray'),plt.title('REFLECT')
plt.subplot(234),plt.imshow(reflect101,'gray'),plt.title('REFLECT_101')
plt.subplot(235),plt.imshow(wrap,'gray'),plt.title('WRAP')
plt.subplot(236),plt.imshow(constant,'gray'),plt.title('CONSTANT')
plt.show()

输出结果为：