图像处理（6）-傅立叶变换在图像处理中的应用、短时傅立叶变换与小波变换

7.3 傅里叶变换在图像处理中的应用

傅里叶变换的实质是将一个信号分离为无穷多个正弦/复指数信号的加成，也就是说，把信号变成正弦信号相加的形式——既然是无穷多个信号相加，那对于非周期信号来说，每个信号的加权应该都是零——但有密度上的差别，你可以对比概率论中的概率密度来思考一下，落到每一个点的概率都是无限小，但这些无限小是有差别的所以，傅里叶变换之后横坐标即为分离出来的正弦信号的频率，纵坐标是加权密度。

那么傅里叶变换在对图片数据处理时有什么用呢？

图像处理中的傅里叶变换的作用对象是二维矩阵。二维矩阵的数学表现形式如下图所示，反应了随着位置的不断改变，灰度值大小变化的情况。我们在此称其为“距离-灰度变化图”：

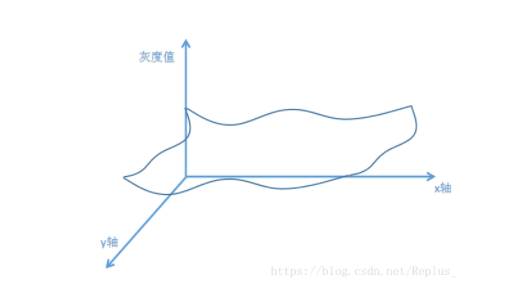
对图片的数据做傅里叶变换，然后增大高频信号的系数就可以提高图像的对比度。同样，相机自动对焦就是通过找图像的高频分量最大的时候，就是对焦好的时候。

在上面我们已经了解了傅里叶级数与傅里叶变换的方式，我们了解到傅里叶分析是对函数在频域上进行分析，时域就是描述数学函数或物理信号对时间的关系。时域（信号对时间的函数）和频域（信号对频率的函数）的变换在数学上是通过积分变换实现的。对周期信号可以直接使用傅里叶变换，对非周期信号则要进行周期扩展，使用拉普拉斯变换。

图像中傅里叶变换的意义

1. 图像的频率是表征图像中灰度变化剧烈程度的指标，是灰度在平面空间上的梯度。如：大面积的沙漠在图像中是一片灰度变化缓慢的区域，对应的频率值很低；而对于地表属性变换剧烈的边缘区域在图像中是一片灰度变化剧烈的区域，对应的频率值很高。傅里叶变换在实际中有非常明显的物理意义，设$f$是一个能量有限的模拟信号，则其傅里叶变换就表示$f$的谱。从纯粹的数学意义上看，傅里叶变换是将一个函数转换为一系列周期函数来处理的。从物理效果来看，傅里叶变化是将图像从空间域转换到频率域，其逆变换是将图像从频率域转换到空间域。换句话说，傅里叶变换的物理意义是将图像的灰度分布函数变换为图像的频率分布函数，逆变换是将图片的频率分布函数变换为灰度分布函数。
2. 傅里叶变换以前，图像是由对在连续空间上的采样得到的一系列点的集合，就是我们现实空间中的一帧，我们习惯用一个二维矩阵表示空间上各点，那么图像其实可以由$z=f(x,y)$来表示。由于空间是三维的，图象是二维的，因此空间中物体在另一维度上的关系就由梯度来表示，这样我们可以通过观察图像得知物体在三维空间中的对应关系。为什么要提梯度？因为实际上对图像进行二维傅里叶变换得到频谱图，就是图像梯度的分布图，当然频谱图上的各点与图像上各点并不存在一一对应的关系。傅里叶频谱图上我们看到的明暗不一的点，实际上图像上某一点与邻域点差异的强弱，即梯度的大小，也是该点的频率大小。通常来说，梯度大则该点的亮度强，否则该点亮度弱。这样通过观察傅里叶变换后的频谱图，也叫功率图，我们首先可以看出，图像的能量分布，如果频谱图中暗的点数更多，那么实际图像是比较柔和的（因为各点与邻域差异都不大，梯度相对较小），反之，如果频谱图中亮的点数多，那么图像一定是尖锐的，边界分明且边界两边像素差异较大。对频谱移频到原点以后，可以看出图像的频率分布是以原点为圆心，对称分布的。将频谱移频到圆心除了可以清晰地看出图像频率以外，还可以分离出有周期性规律的干扰信号，比如正弦干扰。移频到原点的频谱图上可以看出除了中心以外还存在以某一点为中心，对称分布的亮点集合，这个集合就是干扰噪音产生的，这时可以很直观的通过在该位置放置带阻滤波器消除干扰。

我们来看一下图像傅里叶变换后的表现形式，即图片的频谱：

现在，我们就通过类比，来理解这幅图片的各个方向的自变量到底对应信号频谱中的哪个变量。

在信号的频谱中，频率的定义为：单位时间内完成周期性变化的次数。我们可以理解图像进行傅里叶变换结果的频谱中频率的定义为：单位距离内完成周期性变化的次数。由于图像中表达距离的单位是像素大小，所以对这个定义进一步可理解为：N个像素内灰度值完成周期性变化的次数。因此我们大体可以将图像频谱和信号频谱中的自变量联立起来。在信号频谱中的频率是$x$轴，而在图像的频谱中频率是（$x,y$轴构成的）平面。距离原点越远，则说明频率越大。因此，窗口边缘即为高频区域，原点周边即为低频区域。

8. 短时傅里叶变换与小波变换

短时傅里叶变换（Short Time Fourier Transform，STFT）是一个用于信号处理的通用工具。他定义了一个非常有用的时间和频率分布类，其指定了任意信号随时间和频率变化的复数幅度。实际上，计算短时傅里叶变换的过程是把一个较长的时间信号分成相同长度的更短的段，在每个段上计算傅里叶变换，即傅里叶频谱。

那我们为什么要进行短时的傅里叶变换的，这里我们就要说一下傅里叶变换的不足了。

8.1 傅里叶变换的不足

如果要说傅里叶变换的不足，最关键的一点就是傅里叶变换假设前提为信号平稳，但是实际中信号多数为非平稳信号，以频率为例，他要求频率是不随着时间改变的。但是实际情况中往往不能达到这个要求。可以总结为以下几点：

1. 缺乏时间和频率的定位功能
2. 对于非平稳信号的局限性
3. 在时间和频率分辨率上的局限性

8.2 短时傅里叶变换

短时傅里叶变换的策略是通过设置窗格来添加时域信息，我们认为窗格内的信号是平稳的。之后呢我们呢对窗格内的信号分段进行傅里叶变换。

• 优点是可以获得频域信息的同时可以获得时域信息
• 缺点是窗格大小很难设置

STFT的特点有如下几个：

• 窄窗口时间分辨率高，频率分辨率低；宽窗口时间分辨率低，频率分辨率高
• 对于时变的非稳态信号，高频适合小窗口，低频适合大窗口
• 窗口是固定的=。=

这样来看STFT也有它不足的地方，那在这个基础上还可以怎么改进呢，这个就是小波变换。

讲到这里其实傅里叶变换还有一个不足，比如我们把一个常规意义上的图片进行傅里叶变换映射到频率域会变成什么样子呀，我们会得到一个基本上频率域上全都是连续的点，这意味着自然界里的这张图片我们要用各种幅度不同频率不同的正弦波给他凑出来。那我们进行傅里叶变换的初衷是什么呢，其实我们就是想在频域中能更容易的处理这张图片，比如说明暗交替明显的图片我们是可以通过傅里叶变换更好地处理，但是并不是所有图片都是这样的，其实自然的图片更多的是平滑的，不会很突兀的。所以对于这种图片傅里叶变换并没有那么多优势可言。

8.3 小波变换

小波变换与STFT思路接近，但小波变换直接把傅里叶变换的基给改变了——将无限长的三角函数基换成了有限长的会衰减的小波基。这样不仅能够获取频率，还可以定位到时间。

从傅里叶变换到小波变换：

在图片中可以可以更清晰看出对比：

从公式中可以看出，不同于傅里叶变换，变量只有频率$\omega$，小波变换有两个变量：尺度$a$和平移量$\tau$。尺度$a$控制小波函数的伸缩，平移量$\tau$控制小波函数的平移。尺度对应于频率，平移量对应于时间。

不同于傅里叶变换只用正弦波的堆叠去拼凑出一个图像，小波更灵活，可以使用不同的波只要满足要求即可。而且傅里叶变换只能得到一个频谱，而小波变换可以得到一个时频谱。有了小波变换就不用担心信号不稳定了。