图像聚类方法整理-划分式聚类方法

划分式聚类方法需要事先指定簇类的数目或者聚类中心，通过反复迭代，直到最后达到“簇内的点足够近，簇间的点足够远”的目标。经典的划分式聚类方法有K-means及其变体K-means++、bi-Kmeans、kernel K-means等

1. K-means

1.1 经典的K-means算法的流程如下：

1. 选择初始化的$k$个样本作为初始聚类中心$a=a_1,a_2,\dots,a_k$
2. 针对数据集中每个样本$x_i$，计算它到$k$个聚类中心的距离并将其分到距离最小的聚类中心所对应的类中
3. 针对每个类别$a_j$，重新计算它的聚类中心$a_j=\frac{1}{|c_i|}\sum_{x\in c_i}x$（即属于该类的所有样本的质心）
4. 重复上面2，3两步操作，直到达到某个终止条件（迭代次数、最小误差变化等）

 

假设$x_i(i=1,2,\dots,n)$是数据点，$a_j(j=1,2,\dots,k)$是初始化的数据中心，那么目标函数就可以写成：

1.2 优点

• 容易理解，聚类效果不错，虽然是局部最优但是往往局部最优即可
• 处理大数据集的时候，该算法可以保证较好的伸缩性
• 当簇近似高斯分布的时候，效果非常好
• 算法复杂度低

1.3 缺点

• $k$值需要人为设定，不同的$k$值得到的结果不一样
• 对初始质心点敏感，不同的选取方式会得到不同的结果
• 对异常数据敏感
• 样本只能归为一类，不适合多分类的任务
• 不适合太离散的分类、样本类别不平衡的分类、非凸形状的分类

因为离群点或者噪声数据会对均值产生较大的影响，导致中心偏移，因此还需要对数据进行异常点检测。

1.4 $k$值选取

因为$k$值的选取对K-means的影响很大，这也是K-means最大的缺点，常见的选取$k$值得方法有：手肘法、Gap statistic方法

1.4.1 手肘法

手肘法的核心指标是SSE（误差平方和）：

上式中，$C_i$是第$i$个簇类，$p$是$C_i$中的样本点，$a_j$是$C_i$的质心，SSE是所有样本的聚类误差，代表了聚类效果的好坏。

手肘法的核心思想是：随着聚类数k的增大，样本划分会更加精细，每个簇的聚合程度会逐渐提高，那么误差平方和SSE自然会逐渐变小。并且，当k小于真实聚类数时，由于k的增大会大幅增加每个簇的聚合程度，故SSE的下降幅度会很大，而当k到达真实聚类数时，再增加k所得到的聚合程度回报会迅速变小，所以SSE的下降幅度会骤减，然后随着k值的继续增大而趋于平缓，也就是说SSE和k的关系图是一个手肘的形状，而这个肘部对应的k值就是数据的真实聚类数。当然，这也是该方法被称为手肘法的原因。

1.4.2 轮廓系数法

该方法的核心指标是轮廓系数，某个样本点$x_i$的轮廓系数定义如下：

其中，$a$是$x_i$与同簇的其它样本的平均距离，称为凝聚度，$b$是$x_i$与最近簇中所有样本的平均距离，称为分离度。而最近簇的定义是：

其中$p$是某个簇$C_k$中的样本。事实上，就是用$x_i$到某个簇所有的样本平均距离作为衡量该点到该簇的距离后，选择离$x_i$最近的一个簇作为最近簇。

求出所有样本的轮廓系数后再求平均值就得到了平均轮廓系数。平均轮廓系数的取值范围为$[-1,1]$，且簇内样本的距离越近，簇间样本距离越远，平均轮廓系数越大，聚类效果越好。那么，平均轮廓系数最大的$k$便是最佳聚类数。

1.4.3 Gap Statistic

上式中$D_k$为损失函数，这里$E(\log{D_k})$指的是$\log{D_k}$的期望。这个数值通常通过蒙特卡洛模拟产生，我们在样本里所在的区域中按照均匀分布随机产生和原始样本数一样多的随机样本，并对这个随机样本做K-means，从而得到一个$D_k$。如此往复多次，可以得到多个$\log{D_k}$。求这些数值的平均值就得到了$E(\log{D_k})$的近似值。最终可以计算Gap Statistic。而Gap Statistic取得最大值所对应的$k$就是最佳的$k$值。

1.4.4 核函数

基于欧式距离的 K-means 假设了了各个数据簇的数据具有一样的的先验概率并呈现球形分布，但这种分布在实际生活中并不常见。面对非凸的数据分布形状时我们可以引入核函数来优化，这时算法又称为核 K-means 算法，是核聚类方法的一种。核聚类方法的主要思想是通过一个非线性映射，将输入空间中的数据点映射到高位的特征空间中，并在新的特征空间中进行聚类。非线性映射增加了数据点线性可分的概率，从而在经典的聚类算法失效的情况下，通过引入核函数可以达到更为准确的聚类结果。

1.5 ISODATA

ISODATA 的全称是迭代自组织数据分析法。它解决了 K 的值需要预先人为的确定这一缺点。而当遇到高维度、海量的数据集时，人们往往很难准确地估计出 K 的大小。ISODATA 就是针对这个问题进行了改进，它的思想也很直观：当属于某个类别的样本数过少时把这个类别去除，当属于某个类别的样本数过多、分散程度较大时把这个类别分为两个子类别。

ISODATA在K-means算法的基础上，增加对聚类结果的合并和分裂两个操作，当聚类结果某一类中样本数太少，或两个类间的距离太近，或样本类别远大于设定类别数时，进行合并，当聚类结果某一类中样本数太多，或某个类内方差太大，或样本类别远小于设定类别数时，进行分裂。

 

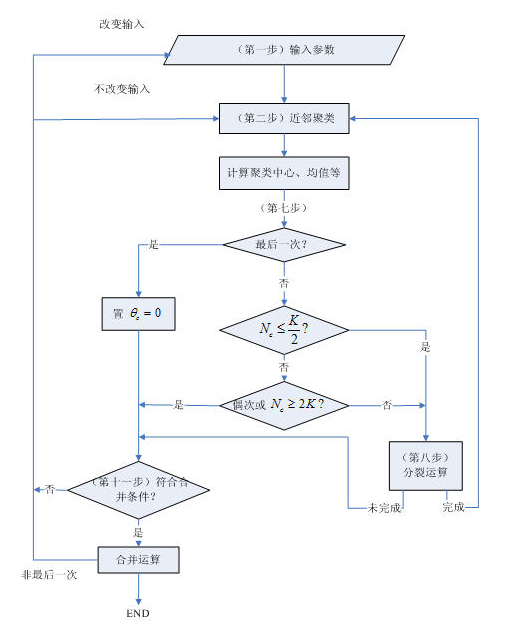
ISODATA算法基本步骤和思路

（1） 选择某些初始值。可选不同的参数指标，也可在迭代过程中人为修改，以将N个模式样本按指标分配到各个聚类中心中去。

（2） 计算各类中诸样本的距离指标函数。

（3）~（5）按给定的要求，将前一次获得的聚类集进行分裂和合并处理（（4）为分裂处理，（5）为合并处理），从而获得新的聚类中心。

（6） 重新进行迭代运算，计算各项指标，判断聚类结果是否符合要求。经过多次迭代后，若结果收敛，则运算结束。

算法流程：

1. 输入$N$个模式样本$\{x_i,i=1,2,\dots.N\}$

   预选$N_c$个初始聚类中心$\{z_1,z_2,\dots,z_{N_c}\}$，它可以不等于所要求的聚类中心的数目，其初始位置可以从样本中任意选取。

   预选：$K=$预期的聚类中心数目；

   $\theta_N=$每一聚类域中最少的样本数目，若少于此数即不作为一个独立的聚类；

   $\theta_S=$一个聚类域中最少的样本数目，若少于此数即不作为一个独立的聚类；

   $\theta_c=$两个聚类中心间的最小距离，若小于此数，两个聚类需进行合并；

   $L=$在一次迭代运算中可以合并的聚类中心的最多对数；

   $I=$迭代运算的次数。

2. 将$N$个模式样本分给最近的聚类$S_j$，假若$D_j=\min\{||x-z_i||,i=1,2,\dots,N_c\}$，即$||x-z_j||$的距离最小，则$x\in S_j$。

3. 如果$S_j$中的样本数目$S_j<\theta_N$，则取消该样本子集，此时$N_c$减去1。

（此处对应基本步骤一）

2. 修正各聚类中心：

5. 计算各聚类域$S_j$中模式样本与各聚类中心间的平均距离

6. 计算全部模式样本和其对应聚类中心的总平均距离

（此处对应基本步骤二）

7. 判别分裂、合并及迭代运算

   1. 若迭代运算次数已达到$I$次，即最后一次迭代，则置$\theta_c=0$，转至第11步。
   2. 若$N_c\le \frac{K}{2}$，即聚类中心的数目小于或等于规定值的一半，则转至第8步，对已有聚类进行分裂处理。
   3. 若迭代运算的次数是偶数次，或$N_c\ge 2K$，不进行分裂处理，转至第11步；否则，转至第8步，进行分裂处理

（以上对应基本步骤三）

8. 计算每个聚类中样本距离的标准差向量

其中向量的各个分量为：

式中，$i=1,2,\dots,n$为样本特征向量的维数，$j=1,2,\dots,N_c$为聚类数，$N_j$为$S_j$中的样本个数。

9. 求每一标准差向量$\{\sigma_j,j=1,2,\dots,N_c\}$中的最大分量，以$\{\sigma_{jmax},=1,2,\dots,N_c\}$代表。

10. 在任一最大分量集$\{\sigma_{jmax},j=1,2,\dots,N_c\}$中，若有$\sigma_{jmax}>\theta_S$，同时又满足如下两个条件之一：

    1. $\bar{D_j}>\bar{D}$和$N_j>2(\theta_N+1)$，即$S_j$中样本总数超过规定值一倍以上，
    2. $N_c\le\frac{K}{2}$

    则将$z_j$分裂为两个新的聚类中心和，且$N_c$加1。中对应于$\sigma_{jmax}$的分量加上$k\sigma_{jmax}$；中对应于$\sigma_{jmax}$的分量减去$k\sigma_{jmax}$。

    如果本步骤完成了分裂运算，则转至第2步，否则继续

（以上对应基本步骤四，进行分裂处理）

11. 计算全部聚类中心的距离

12. 比较$D_{ij}$与$\theta_c$的值，将$D_{ij}<\theta_c$的值按最小距离次序递增排列，即

式中$D_{i1j1}<D_{i2j2}<\cdots<D_{iLjL}$。

13. 将距离为$D_{ikjk}$的两个聚类中心$Z_{ik}$和$Z_{jk}$合并，得到新的中心为：

式中，被合并的两个聚类中心向量分别以其聚类域内的样本数加权，使$Z_k^*$为真正的平均向量。

（以上步骤对应基本步骤五，进行合并处理）

14. 如果是最后一次迭代运算（即第$I$次），则算法结束；否则，若需要操作者改变输入参数，转至第1步；若输入参数不变，转至第2步.在本步运算中，迭代运算的次数每次应加1。

1.6 K-means++

K-means++是针对K-means中初始质心点选取的优化算法，该算法的流程与K-means相似，区别在于对初始质心的选取，该部分的算法流程如下：

1. 随机选取一个中心点$a_1$;
2. 计算数据到之前$n$各聚类中心最远的距离$D(x)$，并以一定概率$\frac{D(x)^2}{\sum{D(x)^2}}$选择新中心点$a_i$；
3. 重复第二步

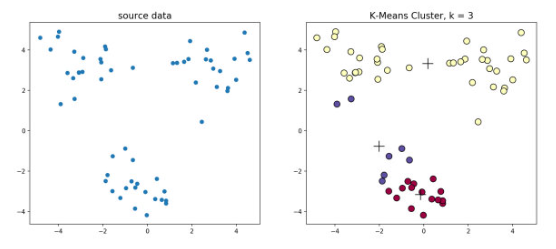
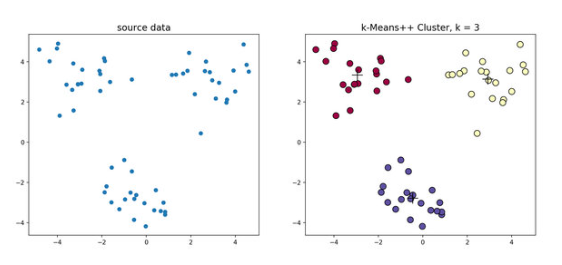
简单来说，K-means++就是选择离已选中心点最远的点。这也比较符合常理，聚类中心当然是互相离得越远越好。

下图为二者对比区别：

缺点

难以并行化。所以K-means II改变取样策略，并非按照K-means++那样每次遍历只取一个样本点，而是每次遍历取样$k$个，重复该取样过程$\log{(n)}$次，则得到$k\log{(n)}$个样本点组成的集合，然后从这些点中选取$k$个。一般情况不需要$\log{(n)}$次取样，5次即可。

2. bi-Kmeans

一种度量聚类效果的指标是SSE(Sum of Squared Error)，他表示聚类后的簇离该簇的聚类中心的平方和，SSE越小，表示聚类效果越好。bi-Kmeans是针对Kmeans算法会陷入局部最优的缺陷进行的改进算法。该算法基于SSE最小化的原理，首先将所有的数据点视为一个簇，然后将该簇一分为二，之后选择其中一个簇继续进行划分，选择哪一个簇进行划分取决于对其划分是否能最大程度地降低SSE的值。

该算法的流程如下：

1. 将所有点视为一个簇

2. 当簇的个数小于$k$时

   1. 对每一个簇

      1. 计算总误差
      2. 在给定的簇上面进行K-means聚类（$k=2$）
      3. 计算将该簇一分为二之后的总误差

   2. 选取使得误差最小的那个簇进行划分操作

该方法是一个全局最优的方法，所以每次计算出来的SSE值基本也是一样的（不排除有部分随即分错的情况）