图像聚类方法整理-基于密度的聚类方法

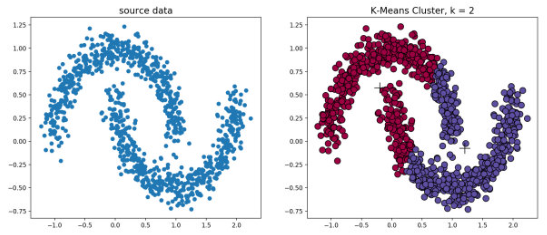
K-means系算法对于凸性数据具有良好的效果，能够根据距离来讲数据分为球状类的簇，但对于非凸形状的数据点就有些无能为力了，当K-means算法在环形数据的聚类时，分类效果如下所示：

1. DBSCAN

从上图可以看出，K-means聚类产生了错误的结果，这个时候就需要用到基于密度的聚类方法了，该方法需要定义两个参数$\varepsilon$和$M$，分别表示密度的邻域半径和邻域密度阈值。

在介绍DBSCAN之前需要先介绍几个概念，考虑集合$X=\{x^{(1)},x^{(2)},\cdots,x^{(n)}\}$，$\varepsilon$表示定义密度的邻域半径，设聚类的邻域密度阈值为$M$，则有以下定义：

• $\varepsilon$邻域

• 密度（desity） $x$的密度为：

• 核心点（core-point）

  设$x\in X$，若$\rho(x)\ge M$，则称$x$为$X$的核心点，记$X$中所有核心点构成的集合为$X_c$，记所有非核心点构成的集合为$X_{nc}$。

• 边界点（border-point）

  若$x\in X_{nc}$，且$\exists y\in X$，满足

  即$x$的$\varepsilon$邻域中存在核心点，则称$x$为$X$的边界点，记$X$中所有的边界点构成的集合为$X_{bd}$。

  此外，边界点也可以这么定义：若$x\in X_{nc}$，且$x$落在某个核心点的$\varepsilon$邻域内，则称$x$为$X$的一个边界点，一个边界点可能同时落入一个或多个核心点的$\varepsilon$邻域。

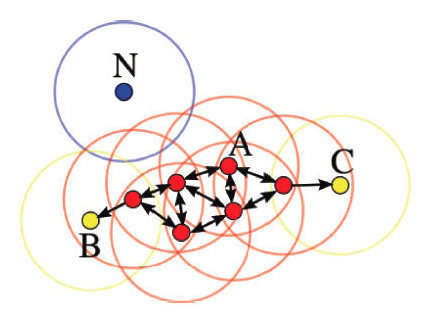
• 噪声点（noise-point）

  若$x$满足：

则称$x$为噪声点。

如下图所示，设$M=3$，则$A$为核心点，$B$、$C$是边界点，而$N$是噪声点。

1.1 算法流程

1. 标记所有对象为unvisited

2. 当有标记对象时

   1. 随机选取一个unvisited对象$p$

   2. 标记$p$为visited

   3. 如果$p$的$\varepsilon$邻域内至少有$M$个对象，则

      1. 创建一个新的簇$C$，并把$p$放入$C$中

      2. 设$N$是$p$的$\varepsilon$邻域内的集合，对$N$中的每个点$p'$

         1. 如果点$p'$是unvisited

            1. 标记$p'$为visited
            2. 如果$p'$的$\varepsilon$邻域至少有$M$个对象，则把这些点添加到$N$
            3. 如果$p'$还不是任何簇的成员，则把$p'$添加到$C$

      3. 保存$C$

   4. 否则标记$p$为噪声

    

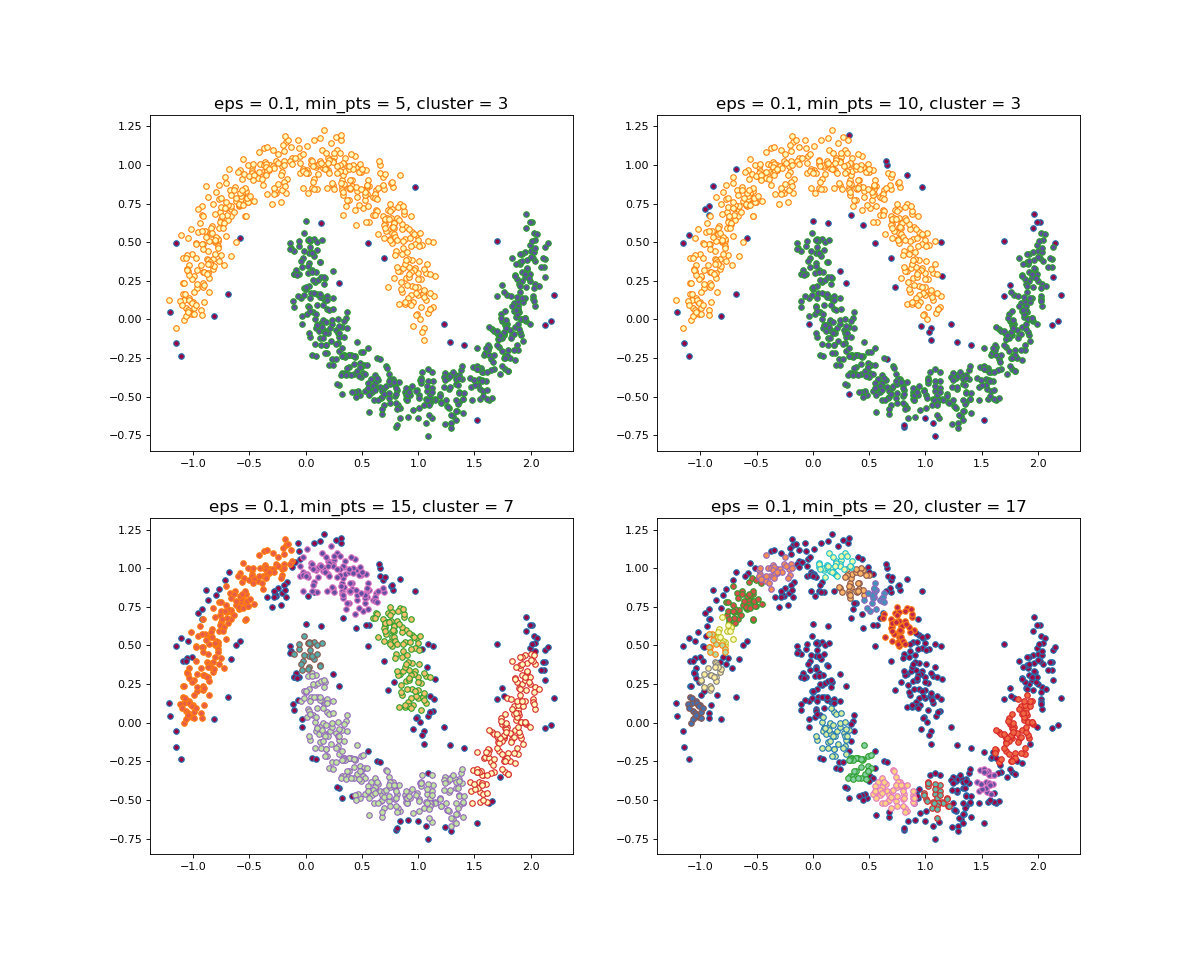
1.2 聚类效果

当设置不同的$\varepsilon$时，会产生不同的结果，如下所示：

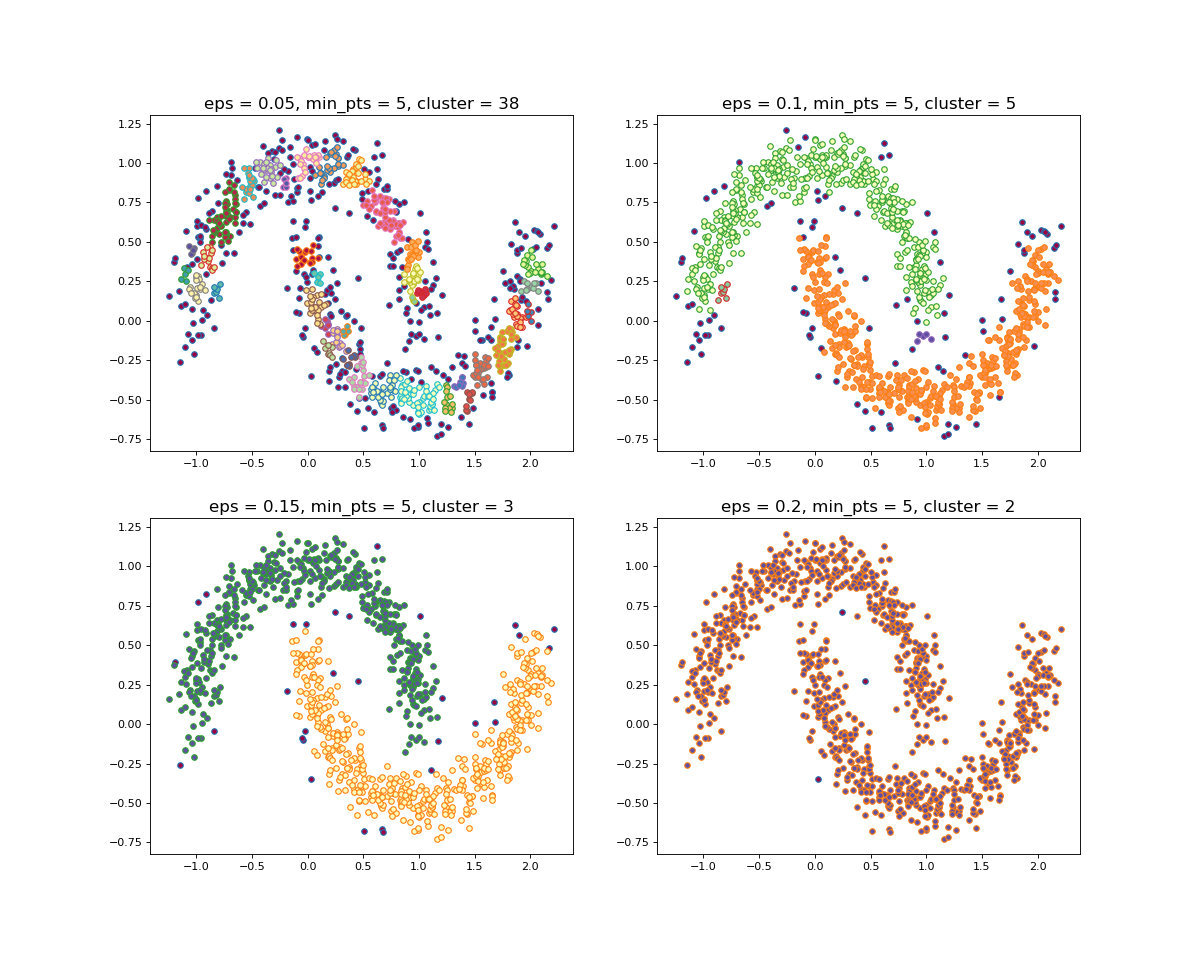
当设置不同的$M$时，会产生不同的结果，如下图所示

1.3 算法特点

1. 需要提前确定$\varepsilon$和$M$的值
2. 不需要提前设置聚类的个数
3. 对初值选取敏感，对噪声不敏感
4. 对米杜不均的数据聚合效果不好

1.3.1 算法总结

• 一个核心思想：基于密度

  直观效果上来讲，DBSCAN算法可以找到样本点的全部密集区域，并把这些密集区域当作一个一个的聚类簇。

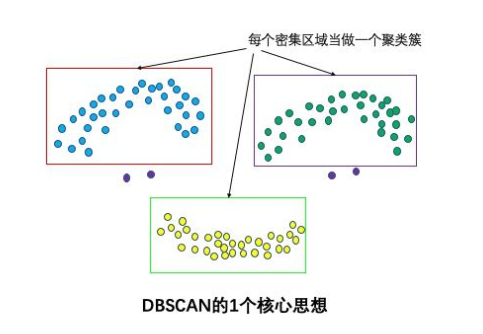
• 两个算法参数：邻域半径$\varepsilon$和最少点数目（邻域密度阈值）minpoint

  算法通过这两个参数来刻画了什么叫做密集，就是说当邻域半径$\varepsilon$内的点的个数大于最少点数目minpoints时，就是密集的。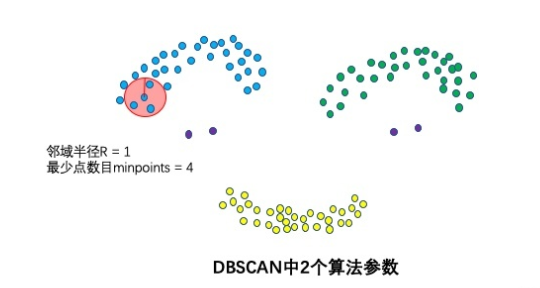

  

• 三种点的类别：核心点，边界点和噪声点

  邻域半径$\varepsilon$内样本点的数量大于等于minpoints的点叫做核心点。不属于核心点但在某个核心点的邻域内的点叫做边界点。既不是核心点也不是边界点的是噪声点。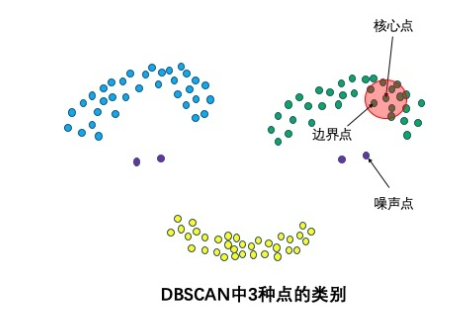

  

• 四种点的关系：密度直达，密度可达，密度相连，非密度相连

  如果$P$为核心点，$Q$在$P$的$R$邻域内，那么称$P$到$Q$密度直达。任何核心点到其自身密度直达，密度直达不具有对称性，如果$P$到$Q$密度直达，那么$Q$到$P$不一定密度直达。

  如果存在核心点$P_2,P_3,\dots,P_n$，且$P_1$到$P_2$密度直达，$P_2$到$P_3$密度直达，$\dots$，$P_{(n-1)}$到$P_n$密度直达，$P_n$到$Q$密度直达，则$P_1$到$Q$密度可达。密度可达也不具有对称性。

  如果存在核心点$S$，使得$S$到$P$和$Q$都密度可达，则$P$和$Q$密度相连。密度相连具有对称性，如果$P$和$Q$密度相连，那么$Q$和$P$也一定密度相连。密度相连的两个点属于同一个聚类簇。

  如果两个点不属于密度相连关系，则两个点非密度相连。非密度相连的两个点属于不同的聚类簇，或者其中存在噪声点。

  

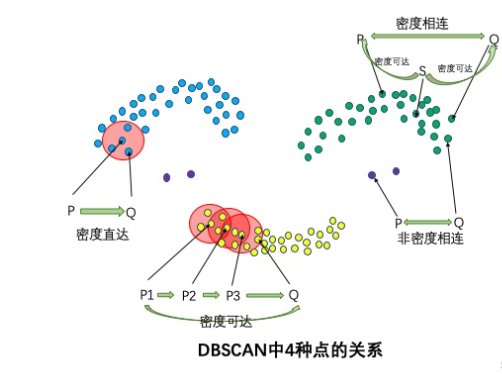
2. Mean-Shift

2.1 Mean-shift的背景

在K-means算法中，最终的聚类效果受初始的聚类中心的影响，K-means++的提出为选择较好的初始聚类中心提供了依据，但是在算法中，簇类数量K仍然需要提前制定，对于类别个数事先未知的数据集，K-means和K-means++还是难以精确求解。

Mean-Shift算法即均值漂移算法，与K-means算法一样基于聚类中心的聚类算法，同时又加入了密度因素。从而能不事先设置簇类数量值。

2.2 算法流程

1. 在未被标记的数据点中随机选择一个点作为中心center
2. 找出离center距离在bandwidth之内的所有点，记作集合$M$，认为这些点属于簇$c$。同时，把这些点属于这个类的概率加1，这个概率将用于最后步骤的分类。
3. 以center为中心点，计算从center开始到集合$M$中每个元素的向量，将这些向量相加，得到向量shift。
4. center = center + shift。即center沿着shift的方向移动，移动距离是$||shift||$。
5. 重复步骤2，3，4，直到shift变得很小（迭代到收敛），记住此时的center。这个迭代过程中所有遇到的点都应该归类到簇$c$。
6. 如果收敛时当前簇$c$的center与其它已经存在的簇$c_2$中心的距离小于阈值，那么把$c_2$与$c$进行合并。否则，把$c$作为新的簇类，增加1类。
7. 重复1，2，3，4，5直到所有的点都被标记访问。
8. 分类：根据每个类，对每个点的访问频率，取访问频率最大的那个类作为当前点的所属类。

2.3 均值漂移向量

对于给定的$d$维空间$R^d$中的$n$个样本点$x_i,i=1,2,\dots,n$，则对于$x$点，其均值漂移向量的基本形式为：